Working with Mesh Data

Note

Several of the operations below rely on the optional dependencies mentioned in Iris’ Mesh Partner Packages.

Operations Summary

Making a Mesh	✨ New
Making a Cube	♻️ Unchanged
Save	♻️ Unchanged
Load	⚠️ Different - UGRID parsing is opt-in
Plotting	⚠️ Different - plot with GeoVista
Region Extraction	⚠️ Different - use GeoVista for mesh analysis
Regridding	⚠️ Different - use iris-esmf-regrid for mesh regridders
Equality	♻️ Unchanged
Combining Cubes	🚧 Support Pending
Arithmetic	♻️ Unchanged

Making a Mesh

✨ New

Already have a file? Consider skipping to Load.

Creating Iris objects from scratch is a highly useful skill for testing code and improving understanding of how Iris works. This knowledge will likely prove particularly useful when converting data into the Iris mesh data model from structured formats and non-UGRID mesh formats.

The objects created in this example will be used where possible in the subsequent example operations on this page.

Code

>>> import numpy as np

>>> from iris.coords import AuxCoord
>>> from iris.experimental.ugrid import Connectivity, Mesh

# Going to create the following mesh
#  (node indices are shown to aid understanding):
#
#  0----1
#  |    |\
#  | +  |+\
#  2----3--4

>>> node_x = AuxCoord(
...     points=[0.0, 5.0, 0.0, 5.0, 8.0],
...     standard_name="longitude",
...     units="degrees_east",
...     long_name="node_x_coordinates",
... )
>>> node_y = AuxCoord(points=[3.0, 3.0, 0.0, 0.0, 0.0], standard_name="latitude")

>>> face_x = AuxCoord([2.0, 6.0], "longitude")
>>> face_y = AuxCoord([1.0, 1.0], "latitude")

>>> edge_node_c = Connectivity(
...     indices=[[0, 1], [0, 2], [1, 3], [1, 4], [2, 3], [3, 4]],
...     cf_role="edge_node_connectivity",
...     attributes={"demo": "Supports every standard CF property"},
... )

# Create some dead-centre edge coordinates.
>>> edge_x, edge_y = [
...     AuxCoord(
...         node_coord.points[edge_node_c.indices_by_location()].mean(axis=1),
...         node_coord.standard_name,
...     )
...     for node_coord in (node_x, node_y)
... ]

>>> face_indices = np.ma.masked_equal([[0, 1, 3, 2], [1, 4, 3, 999]], 999)
>>> face_node_c = Connectivity(
...     indices=face_indices, cf_role="face_node_connectivity"
... )

>>> my_mesh = Mesh(
...     long_name="my_mesh",
...     topology_dimension=2,  # Supports 2D (face) elements.
...     node_coords_and_axes=[(node_x, "x"), (node_y, "y")],
...     connectivities=[edge_node_c, face_node_c],
...     edge_coords_and_axes=[(edge_x, "x"), (edge_y, "y")],
...     face_coords_and_axes=[(face_x, "x"), (face_y, "y")],
... )

>>> print(my_mesh)
Mesh : 'my_mesh'
    topology_dimension: 2
    node
        node_dimension: 'Mesh2d_node'
        node coordinates
            <AuxCoord: longitude / (degrees_east)  [...]  shape(5,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(5,)>
    edge
        edge_dimension: 'Mesh2d_edge'
        edge_node_connectivity: <Connectivity: unknown / (unknown)  [...]  shape(6, 2)>
        edge coordinates
            <AuxCoord: longitude / (unknown)  [...]  shape(6,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(6,)>
    face
        face_dimension: 'Mesh2d_face'
        face_node_connectivity: <Connectivity: unknown / (unknown)  [...]  shape(2, 4)>
        face coordinates
            <AuxCoord: longitude / (unknown)  [...]  shape(2,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(2,)>
    long_name: 'my_mesh'

Making a Cube (with a Mesh)

♻️ Unchanged

Creating a Cube is unchanged; the Mesh is linked via a MeshCoord (see MeshCoords):

Code

>>> import numpy as np

>>> from iris.coords import DimCoord
>>> from iris.cube import Cube, CubeList

>>> vertical_levels = DimCoord([0, 1, 2], "height")

>>> my_cubelist = CubeList()
>>> for conn in (edge_node_c, face_node_c):
...    location = conn.location
...    mesh_coord_x, mesh_coord_y = my_mesh.to_MeshCoords(location)
...    data_shape = (len(conn.indices_by_location()), len(vertical_levels.points))
...    data_array = np.arange(np.prod(data_shape)).reshape(data_shape)
...
...    my_cubelist.append(
...        Cube(
...            data=data_array,
...            long_name=f"{location}_data",
...            units="K",
...            dim_coords_and_dims=[(vertical_levels, 1)],
...            aux_coords_and_dims=[(mesh_coord_x, 0), (mesh_coord_y, 0)],
...        )
...    )

>>> print(my_cubelist)
0: edge_data / (K)                     (-- : 6; height: 3)
1: face_data / (K)                     (-- : 2; height: 3)

>>> for cube in my_cubelist:
...     print(f"{cube.name()}: {cube.mesh.name()}, {cube.location}")
edge_data: my_mesh, edge
face_data: my_mesh, face

>>> print(my_cubelist.extract_cube("edge_data"))
edge_data / (K)                     (-- : 6; height: 3)
    Dimension coordinates:
        height                          -          x
    Mesh coordinates:
        latitude                        x          -
        longitude                       x          -
    Mesh:
        name                        my_mesh
        location                    edge

Save

♻️ Unchanged

Note

UGRID saving support is limited to the NetCDF file format.

The Iris saving process automatically detects if the Cube has an associated Mesh and automatically saves the file in a UGRID-conformant format:

Code

>>> from subprocess import run

>>> from iris import save

>>> cubelist_path = "my_cubelist.nc"
>>> save(my_cubelist, cubelist_path)

>>> ncdump_result = run(["ncdump", "-h", cubelist_path], capture_output=True)
>>> print(ncdump_result.stdout.decode().replace("\t", "    "))
netcdf my_cubelist {
dimensions:
    Mesh2d_node = 5 ;
    Mesh2d_edge = 6 ;
    Mesh2d_face = 2 ;
    height = 3 ;
    my_mesh_face_N_nodes = 4 ;
    my_mesh_edge_N_nodes = 2 ;
variables:
    int my_mesh ;
        my_mesh:cf_role = "mesh_topology" ;
        my_mesh:topology_dimension = 2 ;
        my_mesh:long_name = "my_mesh" ;
        my_mesh:node_coordinates = "longitude latitude" ;
        my_mesh:edge_coordinates = "longitude_0 latitude_0" ;
        my_mesh:face_coordinates = "longitude_1 latitude_1" ;
        my_mesh:face_node_connectivity = "mesh2d_face" ;
        my_mesh:edge_node_connectivity = "mesh2d_edge" ;
    double longitude(Mesh2d_node) ;
        longitude:units = "degrees_east" ;
        longitude:standard_name = "longitude" ;
        longitude:long_name = "node_x_coordinates" ;
    double latitude(Mesh2d_node) ;
        latitude:standard_name = "latitude" ;
    double longitude_0(Mesh2d_edge) ;
        longitude_0:standard_name = "longitude" ;
    double latitude_0(Mesh2d_edge) ;
        latitude_0:standard_name = "latitude" ;
    double longitude_1(Mesh2d_face) ;
        longitude_1:standard_name = "longitude" ;
    double latitude_1(Mesh2d_face) ;
        latitude_1:standard_name = "latitude" ;
    int64 mesh2d_face(Mesh2d_face, my_mesh_face_N_nodes) ;
        mesh2d_face:_FillValue = -1LL ;
        mesh2d_face:cf_role = "face_node_connectivity" ;
        mesh2d_face:start_index = 0LL ;
    int64 mesh2d_edge(Mesh2d_edge, my_mesh_edge_N_nodes) ;
        mesh2d_edge:demo = "Supports every standard CF property" ;
        mesh2d_edge:cf_role = "edge_node_connectivity" ;
        mesh2d_edge:start_index = 0LL ;
    int64 edge_data(Mesh2d_edge, height) ;
        edge_data:long_name = "edge_data" ;
        edge_data:units = "K" ;
        edge_data:mesh = "my_mesh" ;
        edge_data:location = "edge" ;
        edge_data:coordinates = "latitude_0 longitude_0" ;
    int64 height(height) ;
        height:standard_name = "height" ;
    int64 face_data(Mesh2d_face, height) ;
        face_data:long_name = "face_data" ;
        face_data:units = "K" ;
        face_data:mesh = "my_mesh" ;
        face_data:location = "face" ;
        face_data:coordinates = "latitude_1 longitude_1" ;

// global attributes:
        :Conventions = "CF-1.7" ;
}

The iris.experimental.ugrid.save_mesh() function allows Meshes to be saved to file without associated Cubes:

Code

>>> from subprocess import run

>>> from iris.experimental.ugrid import save_mesh

>>> mesh_path = "my_mesh.nc"
>>> save_mesh(my_mesh, mesh_path)

>>> ncdump_result = run(["ncdump", "-h", mesh_path], capture_output=True)
>>> print(ncdump_result.stdout.decode().replace("\t", "    "))
netcdf my_mesh {
dimensions:
    Mesh2d_node = 5 ;
    Mesh2d_edge = 6 ;
    Mesh2d_face = 2 ;
    my_mesh_face_N_nodes = 4 ;
    my_mesh_edge_N_nodes = 2 ;
variables:
    int my_mesh ;
        my_mesh:cf_role = "mesh_topology" ;
        my_mesh:topology_dimension = 2 ;
        my_mesh:long_name = "my_mesh" ;
        my_mesh:node_coordinates = "longitude latitude" ;
        my_mesh:edge_coordinates = "longitude_0 latitude_0" ;
        my_mesh:face_coordinates = "longitude_1 latitude_1" ;
        my_mesh:face_node_connectivity = "mesh2d_face" ;
        my_mesh:edge_node_connectivity = "mesh2d_edge" ;
    double longitude(Mesh2d_node) ;
        longitude:units = "degrees_east" ;
        longitude:standard_name = "longitude" ;
        longitude:long_name = "node_x_coordinates" ;
    double latitude(Mesh2d_node) ;
        latitude:standard_name = "latitude" ;
    double longitude_0(Mesh2d_edge) ;
        longitude_0:standard_name = "longitude" ;
    double latitude_0(Mesh2d_edge) ;
        latitude_0:standard_name = "latitude" ;
    double longitude_1(Mesh2d_face) ;
        longitude_1:standard_name = "longitude" ;
    double latitude_1(Mesh2d_face) ;
        latitude_1:standard_name = "latitude" ;
    int64 mesh2d_face(Mesh2d_face, my_mesh_face_N_nodes) ;
        mesh2d_face:_FillValue = -1LL ;
        mesh2d_face:cf_role = "face_node_connectivity" ;
        mesh2d_face:start_index = 0LL ;
    int64 mesh2d_edge(Mesh2d_edge, my_mesh_edge_N_nodes) ;
        mesh2d_edge:demo = "Supports every standard CF property" ;
        mesh2d_edge:cf_role = "edge_node_connectivity" ;
        mesh2d_edge:start_index = 0LL ;

// global attributes:
        :Conventions = "CF-1.7" ;
}

Load

⚠️ Different - UGRID parsing is opt-in

Note

UGRID loading support is limited to the NetCDF file format.

While Iris’ UGRID support remains experimental, parsing UGRID when loading a file remains optional. To load UGRID data from a file into the Iris mesh data model, use the iris.experimental.ugrid.PARSE_UGRID_ON_LOAD context manager:

Code

>>> from iris import load
>>> from iris.experimental.ugrid import PARSE_UGRID_ON_LOAD

>>> with PARSE_UGRID_ON_LOAD.context():
...     loaded_cubelist = load(cubelist_path)

# Sort CubeList to ensure consistent result.
>>> loaded_cubelist.sort(key=lambda cube: cube.name())
>>> print(loaded_cubelist)
0: edge_data / (K)                     (-- : 6; height: 3)
1: face_data / (K)                     (-- : 2; height: 3)

All the existing loading functionality still operates on UGRID-compliant data - Constraints, callbacks, load_cube() etcetera:

Code

>>> from iris import Constraint, load_cube

>>> with PARSE_UGRID_ON_LOAD.context():
...     ground_cubelist = load(cubelist_path, Constraint(height=0))
...     face_cube = load_cube(cubelist_path, "face_data")

# Sort CubeList to ensure consistent result.
>>> ground_cubelist.sort(key=lambda cube: cube.name())
>>> print(ground_cubelist)
0: edge_data / (K)                     (-- : 6)
1: face_data / (K)                     (-- : 2)

>>> print(face_cube)
face_data / (K)                     (-- : 2; height: 3)
    Dimension coordinates:
        height                          -          x
    Mesh coordinates:
        latitude                        x          -
        longitude                       x          -
    Mesh:
        name                        my_mesh
        location                    face
    Attributes:
        Conventions                 'CF-1.7'

Note

We recommend caution if constraining on coordinates associated with a Mesh. An individual coordinate value might not be shared by any other data points, and using a coordinate range will demand notably higher performance given the size of the dimension versus structured grids (see the data model detail).

The iris.experimental.ugrid.load_mesh() and load_meshes() functions allow only Meshes to be loaded from a file without creating any associated Cubes:

Code

>>> from iris.experimental.ugrid import load_mesh

>>> with PARSE_UGRID_ON_LOAD.context():
...     loaded_mesh = load_mesh(cubelist_path)

>>> print(loaded_mesh)
Mesh : 'my_mesh'
    topology_dimension: 2
    node
        node_dimension: 'Mesh2d_node'
        node coordinates
            <AuxCoord: longitude / (degrees)  [...]  shape(5,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(5,)>
    edge
        edge_dimension: 'Mesh2d_edge'
        edge_node_connectivity: <Connectivity: mesh2d_edge / (unknown)  [...]  shape(6, 2)>
        edge coordinates
            <AuxCoord: longitude / (unknown)  [...]  shape(6,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(6,)>
    face
        face_dimension: 'Mesh2d_face'
        face_node_connectivity: <Connectivity: mesh2d_face / (unknown)  [...]  shape(2, 4)>
        face coordinates
            <AuxCoord: longitude / (unknown)  [...]  shape(2,)>
            <AuxCoord: latitude / (unknown)  [...]  shape(2,)>
    long_name: 'my_mesh'
    var_name: 'my_mesh'

Plotting

⚠️ Different - plot with GeoVista

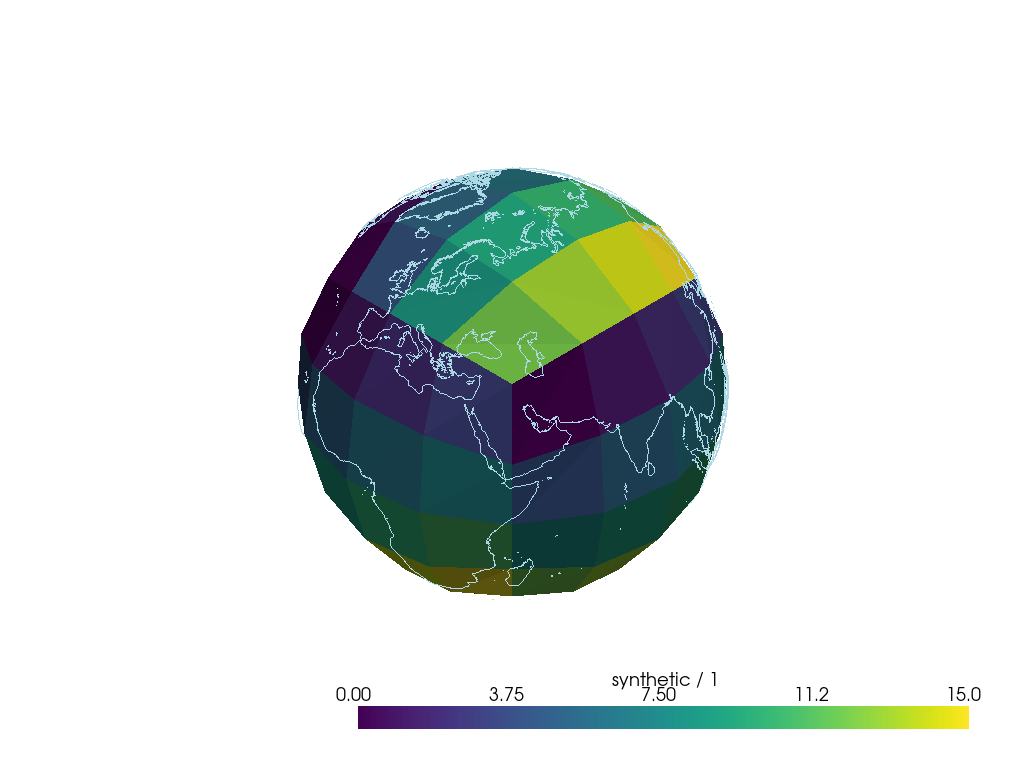
The Cartopy-Matplotlib combination is not optimised for displaying the high number of irregular shapes associated with meshes. Thankfully mesh visualisation is already popular in many other fields (e.g. CGI, gaming, SEM microscopy), so there is a wealth of tooling available, which GeoVista harnesses for cartographic plotting.

GeoVista’s default behaviour is to convert lat-lon information into full XYZ coordinates so the data is visualised on the surface of a 3D globe; 2D projections are also supported. The plots are interactive by default, so it’s easy to explore the data in detail.

Performing GeoVista operations on your Cube is made easy via this convenience: iris.experimental.geovista.cube_to_polydata().

Below is an example of using GeoVista to plot a low-res sample mesh based Cube. For some truly spectacular visualisations of high-res data please see the GeoVista Examples Gallery.

Code

>>> from geovista import GeoPlotter, Transform
>>> from geovista.common import to_cartesian
>>> import matplotlib.pyplot as plt

>>> from iris import load_cube, sample_data_path
>>> from iris.experimental.geovista import cube_to_polydata
>>> from iris.experimental.ugrid import PARSE_UGRID_ON_LOAD

>>> with PARSE_UGRID_ON_LOAD.context():
...     sample_mesh_cube = load_cube(sample_data_path("mesh_C4_synthetic_float.nc"))
>>> print(sample_mesh_cube)
synthetic / (1)                     (-- : 96)
    Mesh coordinates:
        latitude                        x
        longitude                       x
    Mesh:
        name                        Topology data of 2D unstructured mesh
        location                    face
    Attributes:
        NCO                         'netCDF Operators version 4.7.5 (Homepage = http://nco.sf.net, Code = h ...'
        history                     'Mon Apr 12 01:44:41 2021: ncap2 -s synthetic=float(synthetic) mesh_C4_synthetic.nc ...'
        nco_openmp_thread_number    1

# Convert our mesh+data to a PolyData object.
>>> face_polydata = cube_to_polydata(sample_mesh_cube)
>>> print(face_polydata)
PolyData (...
  N Cells:    96
  N Points:   98
  N Strips:   0
  X Bounds:   -1.000e+00, 1.000e+00
  Y Bounds:   -1.000e+00, 1.000e+00
  Z Bounds:   -1.000e+00, 1.000e+00
  N Arrays:   4

# Create the GeoVista plotter and add our mesh+data to it.
>>> my_plotter = GeoPlotter()
>>> my_plotter.add_coastlines()
>>> my_plotter.add_mesh(face_polydata)
>>> my_plotter.show()

Region Extraction

⚠️ Different - use GeoVista for mesh analysis

As described in The Mesh Data Model, indexing for a range along a Cube's mesh_dim() will not provide a contiguous region, since position on the unstructured dimension is unrelated to spatial position. This means that subsetted MeshCoords cannot be reliably interpreted as intended, and subsetting a MeshCoord is therefore set to return an AuxCoord instead - breaking the link between Cube and Mesh:

Code

>>> edge_cube = my_cubelist.extract_cube("edge_data")
>>> print(edge_cube)
edge_data / (K)                     (-- : 6; height: 3)
    Dimension coordinates:
        height                          -          x
    Mesh coordinates:
        latitude                        x          -
        longitude                       x          -
    Mesh:
        name                        my_mesh
        location                    edge

# Sub-setted MeshCoords have become AuxCoords.
>>> print(edge_cube[:-1])
edge_data / (K)                     (-- : 5; height: 3)
    Dimension coordinates:
        height                          -          x
    Auxiliary coordinates:
        latitude                        x          -
        longitude                       x          -

Extracting a region therefore requires extra steps - to determine the spatial position of the data points before they can be analysed as inside/outside the selected region. The recommended way to do this is using tools provided by GeoVista, which is optimised for performant mesh analysis.

Performing GeoVista operations on your Cube is made easy via this convenience: iris.experimental.geovista.cube_to_polydata().

An Iris convenience for regional extraction is also provided: iris.experimental.geovista.extract_unstructured_region(); demonstrated below:

Code

>>> from geovista.geodesic import BBox
>>> from iris import load_cube, sample_data_path
>>> from iris.experimental.geovista import cube_to_polydata, extract_unstructured_region
>>> from iris.experimental.ugrid import PARSE_UGRID_ON_LOAD

>>> with PARSE_UGRID_ON_LOAD.context():
...     sample_mesh_cube = load_cube(sample_data_path("mesh_C4_synthetic_float.nc"))
>>> print(sample_mesh_cube)
synthetic / (1)                     (-- : 96)
    Mesh coordinates:
        latitude                        x
        longitude                       x
    Mesh:
        name                        Topology data of 2D unstructured mesh
        location                    face
    Attributes:
        NCO                         'netCDF Operators version 4.7.5 (Homepage = http://nco.sf.net, Code = h ...'
        history                     'Mon Apr 12 01:44:41 2021: ncap2 -s synthetic=float(synthetic) mesh_C4_synthetic.nc ...'
        nco_openmp_thread_number    1

>>> regional_cube = extract_unstructured_region(
...     cube=sample_mesh_cube,
...     polydata=cube_to_polydata(sample_mesh_cube),
...     region=BBox(lons=[0, 70, 70, 0], lats=[-25, -25, 45, 45]),
...     preference="center",
... )
>>> print(regional_cube)
synthetic / (1)                     (-- : 11)
    Mesh coordinates:
        latitude                        x
        longitude                       x
    Mesh:
        name                        unknown
        location                    face
    Attributes:
        NCO                         'netCDF Operators version 4.7.5 (Homepage = http://nco.sf.net, Code = h ...'
        history                     'Mon Apr 12 01:44:41 2021: ncap2 -s synthetic=float(synthetic) mesh_C4_synthetic.nc ...'
        nco_openmp_thread_number    1

Regridding

⚠️ Different - use iris-esmf-regrid for mesh regridders

Regridding to or from a mesh requires different logic than Iris’ existing regridders, which are designed for structured grids. For this we recommend ESMF’s powerful regridding tools, which integrate with Iris’ mesh data model via the iris-esmf-regrid package.

Regridding is achieved via the esmf_regrid.experimental.unstructured_scheme.MeshToGridESMFRegridder and GridToMeshESMFRegridder classes. Regridding from a source Cube to a target Cube involves initialising and then calling one of these classes. Initialising is done by passing in the source and target Cube as arguments. The regridder is then called by passing the source Cube as an argument. We can demonstrate this with the MeshToGridESMFRegridder:

Code

>>> from esmf_regrid.experimental.unstructured_scheme import MeshToGridESMFRegridder
>>> from iris import load, load_cube
>>> from iris.experimental.ugrid import PARSE_UGRID_ON_LOAD

# You could also download these files from github.com/SciTools/iris-test-data.
>>> from iris.tests import get_data_path
>>> mesh_file = get_data_path(
...     ["NetCDF", "unstructured_grid", "lfric_surface_mean.nc"]
... )
>>> grid_file = get_data_path(
...     ["NetCDF", "regrid", "regrid_template_global_latlon.nc"]
... )

# Load a list of cubes defined on the same Mesh.
>>> with PARSE_UGRID_ON_LOAD.context():
...     mesh_cubes = load(mesh_file)

# Extract a specific cube.
>>> mesh_cube1 = mesh_cubes.extract_cube("sea_surface_temperature")
>>> print(mesh_cube1)
sea_surface_temperature / (K)       (-- : 1; -- : 13824)
    Mesh coordinates:
        latitude                        -       x
        longitude                       -       x
    Auxiliary coordinates:
        time                            x       -
    Cell methods:
        0                           time: mean (interval: 300 s)
        1                           time_counter: mean
    Attributes:
        Conventions                 UGRID
        description                 Created by xios
        interval_operation          300 s
        interval_write              1 d
        name                        lfric_surface
        online_operation            average
        timeStamp                   2020-Feb-07 16:23:14 GMT
        title                       Created by xios
        uuid                        489bcef5-3d1c-4529-be42-4ab5f8c8497b

# Load the target grid.
>>> sample_grid = load_cube(grid_file)
>>> print(sample_grid)
sample_grid / (unknown)             (latitude: 180; longitude: 360)
    Dimension coordinates:
        latitude                             x               -
        longitude                            -               x
    Attributes:
        Conventions                 'CF-1.7'

# Initialise the regridder.
>>> rg = MeshToGridESMFRegridder(mesh_cube1, sample_grid)

# Regrid the mesh cube cube.
>>> result1 = rg(mesh_cube1)
>>> print(result1)
sea_surface_temperature / (K)       (-- : 1; latitude: 180; longitude: 360)
    Dimension coordinates:
        latitude                        -            x               -
        longitude                       -            -               x
    Auxiliary coordinates:
        time                            x            -               -
    Cell methods:
        0                           time: mean (interval: 300 s)
        1                           time_counter: mean
    Attributes:
        Conventions                 UGRID
        description                 Created by xios
        interval_operation          300 s
        interval_write              1 d
        name                        lfric_surface
        online_operation            average
        timeStamp                   2020-Feb-07 16:23:14 GMT
        title                       Created by xios
        uuid                        489bcef5-3d1c-4529-be42-4ab5f8c8497b

Note

All Cube attributes are retained when regridding, so watch out for any attributes that reference the format (there are several in these examples) - you may want to manually remove them to avoid later confusion.

The initialisation process is computationally expensive so we use caching to improve performance. Once a regridder has been initialised, it can be used on any Cube which has been defined on the same Mesh (or on the same grid in the case of GridToMeshESMFRegridder). Since calling a regridder is usually a lot faster than initialising, reusing regridders can save a lot of time. We can demonstrate the reuse of the previously initialised regridder:

Code

# Extract a different cube defined on the same Mesh.
>>> mesh_cube2 = mesh_cubes.extract_cube("precipitation_flux")
>>> print(mesh_cube2)
precipitation_flux / (kg m-2 s-1)   (-- : 1; -- : 13824)
    Mesh coordinates:
        latitude                        -       x
        longitude                       -       x
    Auxiliary coordinates:
        time                            x       -
    Cell methods:
        0                           time: mean (interval: 300 s)
        1                           time_counter: mean
    Attributes:
        Conventions                 UGRID
        description                 Created by xios
        interval_operation          300 s
        interval_write              1 d
        name                        lfric_surface
        online_operation            average
        timeStamp                   2020-Feb-07 16:23:14 GMT
        title                       Created by xios
        uuid                        489bcef5-3d1c-4529-be42-4ab5f8c8497b

# Regrid the new mesh cube using the same regridder.
>>> result2 = rg(mesh_cube2)
>>> print(result2)
precipitation_flux / (kg m-2 s-1)   (-- : 1; latitude: 180; longitude: 360)
    Dimension coordinates:
        latitude                        -            x               -
        longitude                       -            -               x
    Auxiliary coordinates:
        time                            x            -               -
    Cell methods:
        0                           time: mean (interval: 300 s)
        1                           time_counter: mean
    Attributes:
        Conventions                 UGRID
        description                 Created by xios
        interval_operation          300 s
        interval_write              1 d
        name                        lfric_surface
        online_operation            average
        timeStamp                   2020-Feb-07 16:23:14 GMT
        title                       Created by xios
        uuid                        489bcef5-3d1c-4529-be42-4ab5f8c8497b

Support also exists for saving and loading previously initialised regridders - esmf_regrid.experimental.io.save_regridder() and load_regridder() - so that they can be re-used by future scripts.

Equality

♻️ Unchanged

Mesh comparison is supported, and comparing two ‘Mesh-Cubes’ will include a comparison of the respective Meshes, with no extra action needed by the user.

Note

Keep an eye on memory demand when comparing large Meshes, but note that Meshequality is enabled for lazy processing (Real and Lazy Data), so if the Meshes being compared are lazy the process will use less memory than their total size.

Combining Cubes

🚧 Support Pending

Merging or concatenating Cubes (described in Merge and Concatenate) with two different Meshes is not possible - a Cube must be associated with just a single Mesh, and merge/concatenate are not yet capable of combining multiple Meshes into one.

Cubes that include MeshCoords can still be merged/concatenated on dimensions other than the mesh_dim(), since such Cubes will by definition share the same Mesh.

See also

You may wish to investigate iris.experimental.ugrid.recombine_submeshes(), which can be used for a very specific type of Mesh combination not detailed here.

Arithmetic

♻️ Unchanged

Cube Arithmetic (described in Cube Maths) has been extended to handle Cubes that include MeshCoords, and hence have a cube.mesh.

Cubes with meshes can be combined in arithmetic operations like “ordinary” cubes. They can combine with other cubes without that mesh (and its dimension); or with a matching mesh, which may be on a different dimension. Arithmetic can also be performed between a cube with a mesh and a mesh coordinate with a matching mesh.

In all cases, the result will have the same mesh as the input cubes.

Meshes only match if they are fully equal – i.e. they contain all the same coordinates and connectivities, with identical names, units, attributes and data content.