Subsetting a Cube#

The Loading Iris Cubes section of the user guide showed how to load data into multidimensional Iris cubes. However it is often necessary to reduce the dimensionality of a cube down to something more appropriate and/or manageable, or only examine and analyse a subset of data in a dimension.

Iris provides several ways of reducing both the amount of data and/or the number of dimensions in your cube depending on the circumstance. In all cases the subset of a valid cube is itself a valid cube.

Cube Extraction#

A subset of a cube can be “extracted” from a multi-dimensional cube in order to reduce its dimensionality:

>>> import iris
>>> filename = iris.sample_data_path('space_weather.nc')
>>> cube = iris.load_cube(filename, 'electron density')
>>> equator_slice = cube.extract(iris.Constraint(grid_latitude=0))
>>> print(equator_slice)
electron density / (1E11 e/m^3)     (height: 29; grid_longitude: 31)
    Dimension coordinates:
        height                             x                   -
        grid_longitude                     -                   x
    Auxiliary coordinates:
        latitude                           -                   x
        longitude                          -                   x
    Scalar coordinates:
        grid_latitude               0.0 degrees
    Attributes:
        Conventions                 'CF-1.5'

In this example we start with a 3 dimensional cube, with dimensions of height, grid_latitude and grid_longitude, and use iris.Constraint to extract every point where the latitude is 0, resulting in a 2d cube with axes of height and grid_longitude.

Warning

Caution is required when using equality constraints with floating point coordinates such as grid_latitude. Printing the points of a coordinate does not necessarily show the full precision of the underlying number and it is very easy to return no matches to a constraint when one was expected. This can be avoided by using a function as the argument to the constraint:

def near_zero(cell):
   """Returns true if the cell is between -0.1 and 0.1."""
   return -0.1 < cell < 0.1

equator_constraint = iris.Constraint(grid_latitude=near_zero)

Often you will see this construct in shorthand using a lambda function definition:

equator_constraint = iris.Constraint(grid_latitude=lambda cell: -0.1 < cell < 0.1)

The extract method could be applied again to the equator_slice cube to get a further subset.

For example to get a height of 9000 metres at the equator the following line extends the previous example:

equator_height_9km_slice = equator_slice.extract(iris.Constraint(height=9000))
print(equator_height_9km_slice)

The two steps required to get height of 9000 m at the equator can be simplified into a single constraint:

equator_height_9km_slice = cube.extract(iris.Constraint(grid_latitude=0, height=9000))
print(equator_height_9km_slice)

Alternatively, constraints can be combined using &:

cube = iris.load_cube(filename, 'electron density')
equator_constraint = iris.Constraint(grid_latitude=0)
height_constraint = iris.Constraint(height=9000)
equator_height_9km_slice = cube.extract(equator_constraint & height_constraint)

Note

Whilst & is supported, the | that might reasonably be expected is not. Explanation as to why is in the iris.Constraint reference documentation.

For an example of constraining to multiple ranges of the same coordinate to generate one cube, see the iris.Constraint reference documentation.

A common requirement is to limit the value of a coordinate to a specific range, this can be achieved by passing the constraint a function:

def below_9km(cell):
    # return True or False as to whether the cell in question should be kept
    return cell <= 9000

cube = iris.load_cube(filename, 'electron density')
height_below_9km = iris.Constraint(height=below_9km)
below_9km_slice = cube.extract(height_below_9km)

As we saw in Loading Iris Cubes the result of iris.load() is a CubeList. The extract method also exists on a CubeList and behaves in exactly the same way as loading with constraints:

>>> import iris
>>> air_temp_and_fp_6 = iris.Constraint('air_potential_temperature', forecast_period=6)
>>> level_10 = iris.Constraint(model_level_number=10)
>>> filename = iris.sample_data_path('uk_hires.pp')
>>> cubes = iris.load(filename).extract(air_temp_and_fp_6 & level_10)
>>> print(cubes)
0: air_potential_temperature / (K)     (grid_latitude: 204; grid_longitude: 187)
>>> print(cubes[0])
air_potential_temperature / (K)     (grid_latitude: 204; grid_longitude: 187)
    Dimension coordinates:
        grid_latitude                             x                    -
        grid_longitude                            -                    x
    Auxiliary coordinates:
        surface_altitude                          x                    x
    Derived coordinates:
        altitude                                  x                    x
    Scalar coordinates:
        forecast_period             6.0 hours
        forecast_reference_time     2009-11-19 04:00:00
        level_height                395.0 m, bound=(360.0, 433.3332) m
        model_level_number          10
        sigma                       0.9549927, bound=(0.9589389, 0.95068014)
        time                        2009-11-19 10:00:00
    Attributes:
        STASH                       m01s00i004
        source                      'Data from Met Office Unified Model'
        um_version                  '7.3'

Cube attributes can also be part of the constraint criteria. Supposing a cube attribute of STASH existed, as is the case when loading PP files, then specific STASH codes can be filtered:

filename = iris.sample_data_path('uk_hires.pp')
level_10_with_stash = iris.AttributeConstraint(STASH='m01s00i004') & iris.Constraint(model_level_number=10)
cubes = iris.load(filename).extract(level_10_with_stash)

Constraining a Circular Coordinate Across its Boundary#

Occasionally you may need to constrain your cube with a region that crosses the boundary of a circular coordinate (this is often the meridian or the dateline / antimeridian). An example use-case of this is to extract the entire Pacific Ocean from a cube whose longitudes are bounded by the dateline.

This functionality cannot be provided reliably using constraints. Instead you should use the functionality provided by cube.intersection to extract this region.

Constraining on Time#

Iris follows NetCDF-CF rules in representing time coordinate values as normalised, purely numeric, values which are normalised by the calendar specified in the coordinate’s units (e.g. “days since 1970-01-01”). However, when constraining by time we usually want to test calendar-related aspects such as hours of the day or months of the year, so Iris provides special features to facilitate this.

Firstly, when Iris evaluates iris.Constraint expressions, it will convert time-coordinate values (points and bounds) from numbers into datetime-like objects for ease of calendar-based testing.

>>> filename = iris.sample_data_path('uk_hires.pp')
>>> cube_all = iris.load_cube(filename, 'air_potential_temperature')
>>> print('All times :\n' + str(cube_all.coord('time')))
All times :
DimCoord :  time / (hours since 1970-01-01 00:00:00, standard calendar)
    points: [2009-11-19 10:00:00, 2009-11-19 11:00:00, 2009-11-19 12:00:00]
    shape: (3,)
    dtype: float64
    standard_name: 'time'
>>> # Define a function which accepts a datetime as its argument (this is simplified in later examples).
>>> hour_11 = iris.Constraint(time=lambda cell: cell.point.hour == 11)
>>> cube_11 = cube_all.extract(hour_11)
>>> print('Selected times :\n' + str(cube_11.coord('time')))
Selected times :
DimCoord :  time / (hours since 1970-01-01 00:00:00, standard calendar)
    points: [2009-11-19 11:00:00]
    shape: (1,)
    dtype: float64
    standard_name: 'time'

Secondly, the iris.time module provides flexible time comparison facilities. An iris.time.PartialDateTime object can be compared to objects such as datetime.datetime instances, and this comparison will then test only those ‘aspects’ which the PartialDateTime instance defines:

>>> import datetime
>>> from iris.time import PartialDateTime
>>> dt = datetime.datetime(2011, 3, 7)
>>> print(dt > PartialDateTime(year=2010, month=6))
True
>>> print(dt > PartialDateTime(month=6))
False

These two facilities can be combined to provide straightforward calendar-based time selections when loading or extracting data.

The previous constraint example can now be written as:

>>> the_11th_hour = iris.Constraint(time=iris.time.PartialDateTime(hour=11))
>>> print(iris.load_cube(
...     iris.sample_data_path('uk_hires.pp'),
...    'air_potential_temperature' & the_11th_hour).coord('time'))
DimCoord :  time / (hours since 1970-01-01 00:00:00, standard calendar)
    points: [2009-11-19 11:00:00]
    shape: (1,)
    dtype: float64
    standard_name: 'time'

It is common that a cube will need to be constrained between two given dates. In the following example we construct a time sequence representing the first day of every week for many years:

>>> print(long_ts.coord('time'))
DimCoord :  time / (days since 2007-04-09, standard calendar)
    points: [
        2007-04-09 00:00:00, 2007-04-16 00:00:00, ...,
        2010-02-08 00:00:00, 2010-02-15 00:00:00]
    shape: (150,)
    dtype: int64
    standard_name: 'time'

Given two dates in datetime format, we can select all points between them. Instead of constraining at loaded time, we already have the time coord so we constrain that coord using iris.cube.Cube.extract

>>> d1 = datetime.datetime.strptime('20070715T0000Z', '%Y%m%dT%H%MZ')
>>> d2 = datetime.datetime.strptime('20070825T0000Z', '%Y%m%dT%H%MZ')
>>> st_swithuns_daterange_07 = iris.Constraint(
...     time=lambda cell: d1 <= cell.point < d2)
>>> within_st_swithuns_07 = long_ts.extract(st_swithuns_daterange_07)
>>> print(within_st_swithuns_07.coord('time'))
DimCoord :  time / (days since 2007-04-09, standard calendar)
    points: [
        2007-07-16 00:00:00, 2007-07-23 00:00:00, 2007-07-30 00:00:00,
        2007-08-06 00:00:00, 2007-08-13 00:00:00, 2007-08-20 00:00:00]
    shape: (6,)
    dtype: int64
    standard_name: 'time'

Alternatively, we may rewrite this using iris.time.PartialDateTime objects.

>>> pdt1 = PartialDateTime(year=2007, month=7, day=15)
>>> pdt2 = PartialDateTime(year=2007, month=8, day=25)
>>> st_swithuns_daterange_07 = iris.Constraint(
...     time=lambda cell: pdt1 <= cell.point < pdt2)
>>> within_st_swithuns_07 = long_ts.extract(st_swithuns_daterange_07)
>>> print(within_st_swithuns_07.coord('time'))
DimCoord :  time / (days since 2007-04-09, standard calendar)
    points: [
        2007-07-16 00:00:00, 2007-07-23 00:00:00, 2007-07-30 00:00:00,
        2007-08-06 00:00:00, 2007-08-13 00:00:00, 2007-08-20 00:00:00]
    shape: (6,)
    dtype: int64
    standard_name: 'time'

A more complex example might require selecting points over an annually repeating date range. We can select points within a certain part of the year, in this case between the 15th of July through to the 25th of August. By making use of PartialDateTime this becomes simple:

>>> st_swithuns_daterange = iris.Constraint(
...     time=lambda cell: PartialDateTime(month=7, day=15) <= cell.point < PartialDateTime(month=8, day=25))
>>> within_st_swithuns = long_ts.extract(st_swithuns_daterange)
...
>>> # Note: using summary(max_values) to show more of the points
>>> print(within_st_swithuns.coord('time').summary(max_values=100))
DimCoord :  time / (days since 2007-04-09, standard calendar)
    points: [
        2007-07-16 00:00:00, 2007-07-23 00:00:00, 2007-07-30 00:00:00,
        2007-08-06 00:00:00, 2007-08-13 00:00:00, 2007-08-20 00:00:00,
        2008-07-21 00:00:00, 2008-07-28 00:00:00, 2008-08-04 00:00:00,
        2008-08-11 00:00:00, 2008-08-18 00:00:00, 2009-07-20 00:00:00,
        2009-07-27 00:00:00, 2009-08-03 00:00:00, 2009-08-10 00:00:00,
        2009-08-17 00:00:00, 2009-08-24 00:00:00]
    shape: (17,)
    dtype: int64
    standard_name: 'time'

Notice how the dates printed are between the range specified in the st_swithuns_daterange and that they span multiple years.

The above examples involve constraining on the points of the time coordinate. Constraining on bounds can be done in the following way:

filename = iris.sample_data_path('ostia_monthly.nc')
cube = iris.load_cube(filename, 'surface_temperature')
dtmin = datetime.datetime(2008, 1, 1)
cube.extract(iris.Constraint(time = lambda cell: any(bound > dtmin for bound in cell.bound)))

The above example constrains to cells where either the upper or lower bound occur after 1st January 2008.

Cube Masking#

Masking from a shapefile#

Often we want to perform some kind of analysis over a complex geographical feature e.g.,

over only land/sea points
over a continent, country, or list of countries
over a river watershed or lake basin
over states or administrative regions of a country

These geographical features can often be described by ESRI Shapefiles. Shapefiles are a file format first developed for GIS software in the 1990s, and Natural Earth maintain a large freely usable database of shapefiles of many geographical and political divisions, accessible via cartopy. Users may also provide their own custom shapefiles for cartopy to load, or their own underlying geometry in the same format as a shapefile geometry.

These shapefiles can be used to mask an iris cube, so that any data outside the bounds of the shapefile is hidden from further analysis or plotting.

First, we load the correct shapefile from NaturalEarth via the Cartopy_shapereader instructions. Here we get one for Brazil. The .geometry attribute of the records in the reader contain the Shapely polygon we’re interested in. They contain the coordinates that define the polygon (or set of lines) being masked and once we have those we just need to provide them to the iris.util.mask_cube_from_shapefile function. This returns a copy of the cube with a numpy.masked_array as the data payload, where the data outside the shape is hidden by the masked array. We can see this in the following example.

"""Global cube masked to Brazil and plotted with quickplot."""

import cartopy.io.shapereader as shpreader
import matplotlib.pyplot as plt

import iris
import iris.quickplot as qplt
from iris.util import mask_cube_from_shapefile

country_shp_reader = shpreader.Reader(
    shpreader.natural_earth(
        resolution="110m", category="cultural", name="admin_0_countries"
    )
)
brazil_shp = [
    country.geometry
    for country in country_shp_reader.records()
    if "Brazil" in country.attributes["NAME_LONG"]
][0]

cube = iris.load_cube(iris.sample_data_path("air_temp.pp"))
brazil_cube = mask_cube_from_shapefile(cube, brazil_shp)

qplt.pcolormesh(brazil_cube)
plt.show()

(Source code, png)

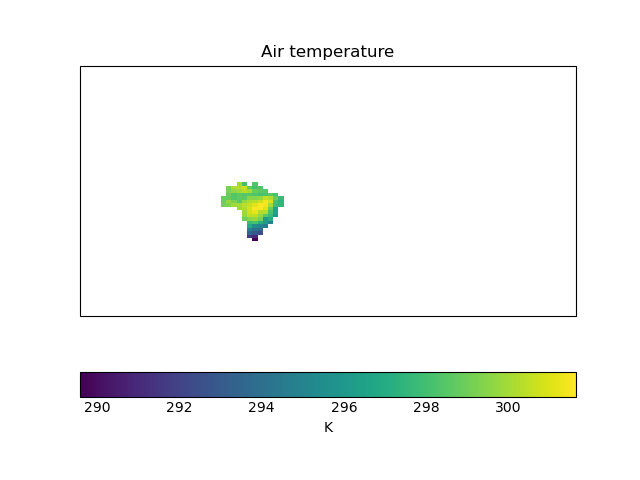
We can see that the dimensions of the cube haven’t changed - the plot is still global. But only the data over Brazil is plotted - the rest has been masked out.

Note

While Iris will try to dynamically adjust the shapefile to mask cubes of different projections, it can struggle with rotated pole projections and cubes with Meridians not at 0° Converting your Cube’s coordinate system may help if you get a fully masked cube as the output from this function unexpectedly.

Cube Iteration#

It is not possible to directly iterate over an Iris cube. That is, you cannot use code such as for x in cube:. However, you can iterate over cube slices, as this section details.

A useful way of dealing with a Cube in its entirety is by iterating over its layers or slices. For example, to deal with a 3 dimensional cube (z,y,x) you could iterate over all 2 dimensional slices in y and x which make up the full 3d cube.:

import iris
filename = iris.sample_data_path('hybrid_height.nc')
cube = iris.load_cube(filename)
print(cube)
for yx_slice in cube.slices(['grid_latitude', 'grid_longitude']):
   print(repr(yx_slice))

As the original cube had the shape (15, 100, 100) there were 15 latitude longitude slices and hence the line print(repr(yx_slice)) was run 15 times.

Note

The order of latitude and longitude in the list is important; had they been swapped the resultant cube slices would have been transposed.

For further information see Cube.slices.

This method can handle n-dimensional slices by providing more or fewer coordinate names in the list to slices:

import iris
filename = iris.sample_data_path('hybrid_height.nc')
cube = iris.load_cube(filename)
print(cube)
for i, x_slice in enumerate(cube.slices(['grid_longitude'])):
   print(i, repr(x_slice))

The Python function enumerate() is used in this example to provide an incrementing variable i which is printed with the summary of each cube slice. Note that there were 1500 1d longitude cubes as a result of slicing the 3 dimensional cube (15, 100, 100) by longitude (i starts at 0 and 1500 = 15 * 100).

Hint

It is often useful to get a single 2d slice from a multidimensional cube in order to develop a 2d plot function, for example. This can be achieved by using the next() function on the result of slices:

first_slice = next(cube.slices(['grid_latitude', 'grid_longitude']))

Once the your code can handle a 2d slice, it is then an easy step to loop over all 2d slices within the bigger cube using the slices method.

Cube Indexing#

In the same way that you would expect a numeric multidimensional array to be indexed to take a subset of your original array, you can index a Cube for the same purpose.

Here are some examples of array indexing in numpy:

import numpy as np
# create an array of 12 consecutive integers starting from 0
a = np.arange(12)
print(a)

print(a[0])     # first element of the array

print(a[-1])    # last element of the array

print(a[0:4])   # first four elements of the array (the same as a[:4])

print(a[-4:])   # last four elements of the array

print(a[::-1])  # gives all of the array, but backwards

# Make a 2d array by reshaping a
b = a.reshape(3, 4)
print(b)

print(b[0, 0])  # first element of the first and second dimensions

print(b[0])     # first element of the first dimension (+ every other dimension)

# get the second element of the first dimension and all of the second dimension
# in reverse, by steps of two.
print(b[1, ::-2])

Similarly, Iris cubes have indexing capability:

import iris
filename = iris.sample_data_path('hybrid_height.nc')
cube = iris.load_cube(filename)

print(cube)

# get the first element of the first dimension (+ every other dimension)
print(cube[0])

# get the last element of the first dimension (+ every other dimension)
print(cube[-1])

# get the first 4 elements of the first dimension (+ every other dimension)
print(cube[0:4])

# Get the first element of the first and third dimension (+ every other dimension)
print(cube[0, :, 0])

# Get the second element of the first dimension and all of the second dimension
# in reverse, by steps of two.
print(cube[1, ::-2])