Merge and Concatenate¶
We saw in the Loading Iris Cubes chapter that Iris tries to load as few cubes as
possible. This is done by collecting together multiple fields with a shared standard
name (and other key metadata) into a single multidimensional cube. The processes that
perform this behaviour in Iris are known as merge and concatenate.
This chapter describes the merge and concatenate processes; it explains
why common issues occur when using them and gives advice on how prevent these
issues from occurring.
Both merge and concatenate take multiple cubes as input and
result in fewer cubes as output. The following diagram illustrates the two processes:

There is one major difference between the merge and concatenate processes.
The
mergeprocess combines multiple input cubes into a single resultant cube with new dimensions created from the scalar coordinate values of the input cubes.The
concatenateprocess combines multiple input cubes into a single resultant cube with the same number of dimensions as the input cubes, but with the length of one or more dimensions extended by joining together sequential dimension coordinates.
Let’s imagine 28 individual cubes representing the
temperature at a location (y, x); one cube for each day of February. We can use
merge() to combine the 28 (y, x) cubes into
a single (t, y, x) cube, where the length of the t dimension is 28.
Now imagine 12 individual cubes representing daily temperature at a time and
location (t, y, x); one cube for each month in the year. We can use
concatenate() to combine the 12
(t, y, x) cubes into a single (t, y, x) cube, where the length
of the t dimension is now 365.
Merge¶
We’ve seen that the merge process combines multiple input cubes into a
single resultant cube with new dimensions created from the
scalar coordinate values of the input cubes.
In order to construct new coordinates for the new dimensions, the merge process requires input cubes
with scalar coordinates that can be combined together into monotonic sequences.
The order of the input cubes does not affect the merge process.
The merge process can produce a cube that has more than one new dimension,
if the scalar coordinate sequences form an orthogonal basis.
Important
The shape, metadata, attributes, coordinates, coordinates metadata, fill value and other aspects of the input cubes must be consistent across all of the input cubes.
The merge process will fail if these are not consistent. Such failures are
covered in the Common Issues With Merge and Concatenate section.
The merge process can be accessed using two methods. The two methods are
merge() and merge_cube(),
which are described below.
Using CubeList.merge¶
The CubeList.merge method operates on a list
of cubes and returns a new CubeList containing the cubes
that have been merged.
Let’s have a look at the merge() method in operation.
In this example we have a list of three lateral (x, y) cubes in a
variable called cubes, each with a scalar z coordinate of
differing value. We can merge these cubes by stacking the scalar z coordinates to
make a new z dimension coordinate:
>>> print(cubes)
0: air_temperature / (kelvin) (y: 4; x: 5)
1: air_temperature / (kelvin) (y: 4; x: 5)
2: air_temperature / (kelvin) (y: 4; x: 5)
>>> print(cubes[0])
air_temperature / (kelvin) (y: 4; x: 5)
...
Scalar coordinates:
z 1 meters
>>> print(cubes[1])
air_temperature / (kelvin) (y: 4; x: 5)
...
Scalar coordinates:
z 2 meters
>>> print(cubes[2])
air_temperature / (kelvin) (y: 4; x: 5)
Dimension coordinates:
y x -
x - x
Scalar coordinates:
z 3 meters
>>> print(cubes.merge())
0: air_temperature / (kelvin) (z: 3; y: 4; x: 5)
The following diagram illustrates what has taken place in this example:
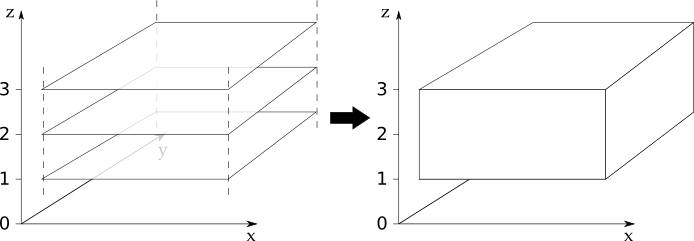
The diagram illustrates that we have three input cubes of identical shape
that stack on the z dimension.
After merging our three input cubes we get a new CubeList containing
one cube with a new z coordinate.
Using CubeList.merge_cube¶
The merge_cube() method guarantees that exactly one cube will be returned
as a result of merging the input cubes.
If merge_cube() cannot fulfil this guarantee, a descriptive error
will be raised providing details to help diagnose the differences between the input cubes.
In contrast, the merge() method makes no check on the number of cubes returned.
To demonstrate the differences between merge()
and merge_cube(), let’s return to our three cubes
from the earlier merge example.
For the purposes of this example a Conventions attribute has been added to the first
cube’s attributes dictionary.
Remember that the attributes must be consistent across all cubes in order to merge
into a single cube:
>>> print(cubes)
0: air_temperature / (kelvin) (y: 4; x: 5)
1: air_temperature / (kelvin) (y: 4; x: 5)
2: air_temperature / (kelvin) (y: 4; x: 5)
>>> print(cubes[0].attributes)
{'Conventions': 'CF-1.5'}
>>> print(cubes[1].attributes)
{}
>>> print(cubes[2].attributes)
{}
>>> print(cubes.merge())
0: air_temperature / (kelvin) (y: 4; x: 5)
1: air_temperature / (kelvin) (z: 2; y: 4; x: 5)
>>> print(cubes.merge_cube())
Traceback (most recent call last):
...
raise iris.exceptions.MergeError(msgs)
iris.exceptions.MergeError: failed to merge into a single cube.
cube.attributes keys differ: 'Conventions'
Note that merge() returns two cubes here.
All the cubes that can be merged have been merged. Any cubes that can’t be merged are
included unchanged in the returned CubeList.
When merge_cube() is called on cubes it raises a
descriptive error that highlights the difference in the attributes dictionaries.
It is this difference that is preventing cubes being merged into a
single cube. An example of fixing an issue like this can be found in the
Common Issues With Merge and Concatenate section.
Merge in Iris Load¶
The CubeList’s merge() method is used internally
by the three main Iris load functions introduced in Loading Iris Cubes.
For file formats such as GRIB and PP, which store fields as many
individual 2D arrays, Iris loading uses the merge process to produce a
more intuitive higher dimensional cube of each phenomenon where possible.
Sometimes the merge process doesn’t behave as expected. In almost all
cases this is due to the input cubes containing unexpected or inconsistent metadata.
For this reason, a fourth Iris file loading function, iris.load_raw(), exists.
The load_raw() function is intended as a diagnostic tool that can be used to
load cubes from files without the merge process taking place. The return value of
iris.load_raw() is always a CubeList instance.
You can then call the merge_cube() method on this returned
CubeList to help identify merge related load issues.
Concatenate¶
We’ve seen that the concatenate process combines multiple input cubes into a
single resultant cube with the same number of dimensions as the input cubes,
but with the length of one or more dimensions extended by joining together
sequential dimension coordinates.
In order to extend the dimensions lengths, the concatenate process requires input cubes
with dimension coordinates that can be combined together into monotonic sequences.
The order of the input cubes does not affect the concatenate process.
Important
The shape, metadata, attributes, coordinates, coordinates metadata, fill value and other aspects of the input cubes must be consistent across all of the input cubes.
The concatenate process will fail if these are not consistent. Such failures are
covered in the Common Issues With Merge and Concatenate section.
The concatenate process can be accessed using two methods. The two methods are
concatenate() and concatenate_cube(),
which are described below.
Using CubeList.concatenate¶
The CubeList.concatenate method operates on a list
of cubes and returns a new CubeList containing the cubes
that have been concatenated.
Let’s have a look at the concatenate() method in operation.
In the example below we have three 3D (t, y, x) cubes whose t coordinates
have sequentially increasing ranges.
These cubes can be concatenated by combining the t coordinates of the input
cubes to form a new cube with an extended t coordinate:
>>> print(cubes)
0: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
1: air_temperature / (kelvin) (t: 28; y: 3; x: 4)
2: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
>>> print(cubes.concatenate())
0: air_temperature / (kelvin) (t: 90; y: 3; x: 4)
The following diagram illustrates what has taken place in this example:
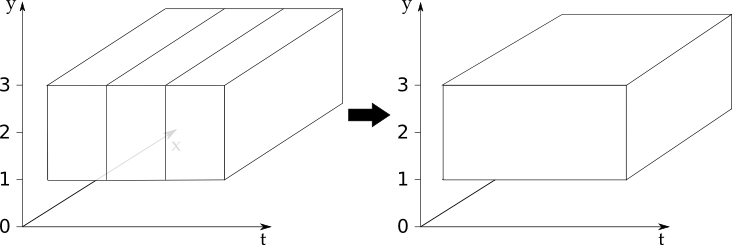
The diagram illustrates that we have three 3D input cubes
that line up on the t dimension.
After concatenating our three input cubes we get a new CubeList
containing one cube with an extended t coordinate.
Using CubeList.concatenate_cube¶
The concatenate_cube() method guarantees that exactly one
cube will be returned as a result of concatenating the input cubes.
If concatenate_cube() cannot fulfil this guarantee, a descriptive error
will be raised providing details to help diagnose the differences between the input cubes.
In contrast, the concatenate() method makes no check on the number
of cubes returned.
To demonstrate the differences between concatenate()
and concatenate_cube(), let’s return to our three cubes
from the earlier concatenate example.
For the purposes of this example we’ll add a History attribute to the first
cube’s attributes dictionary.
Remember that the attributes must be consistent across all cubes in order to
concatenate into a single cube:
>>> print(cubes)
0: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
1: air_temperature / (kelvin) (t: 28; y: 3; x: 4)
2: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
>>> print(cubes[0].attributes)
{'History': 'Created 2010-06-30'}
>>> print(cubes[1].attributes)
{}
>>> print(cubes.concatenate())
0: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
1: air_temperature / (kelvin) (t: 59; y: 3; x: 4)
>>> print(cubes.concatenate_cube())
Traceback (most recent call last):
...
raise iris.exceptions.ConcatenateError(msgs)
iris.exceptions.ConcatenateError: failed to concatenate into a single cube.
Cube metadata differs for phenomenon: air_temperature
Note that concatenate() returns two cubes here.
All the cubes that can be concatenated have been concatenated. Any cubes that can’t be concatenated are
included unchanged in the returned CubeList.
When concatenate_cube() is called on cubes it raises a
descriptive error that highlights the difference in the attributes dictionaries.
It is this difference that is preventing cubes being concatenated into a
single cube. An example of fixing an issue like this can be found in the
Common Issues With Merge and Concatenate section.
Common Issues With Merge and Concatenate¶
The Iris algorithms that drive merge() and
concatenate() are complex and depend
on a number of different elements of the input cubes being consistent across
all input cubes.
If this consistency is not maintained then the
merge() or
concatenate() process can fail in a
seemingly arbitrary manner.
The methods merge_cube() and
concatenate_cube()
were introduced to Iris to help you locate differences in input cubes
that prevent the input cubes merging or concatenating.
Nevertheless, certain difficulties with using
merge() and
concatenate() occur frequently.
This section describes these common difficulties, why they arise and
what you can do to avoid them.
Merge¶
Attributes Mismatch
Differences in the attributes the input cubes probably
cause the greatest amount of merge-related difficulties.
In recognition of this, Iris has a helper function,
equalise_attributes(), to equalise
attributes differences in the input cubes.
Note
The functionality provided by iris.util.describe_diff() and
iris.cube.Cube.is_compatible() are not designed to give user
indication of whether two cubes can be merged.
To demonstrate using equalise_attributes(),
let’s return to our non-merging list of input cubes from the merge_cube example
from earlier.
We’ll call equalise_attributes() on the
input cubes before merging the input cubes using merge_cube():
>>> from iris.util import equalise_attributes
>>> print(cubes)
0: air_temperature / (kelvin) (y: 4; x: 5)
1: air_temperature / (kelvin) (y: 4; x: 5)
2: air_temperature / (kelvin) (y: 4; x: 5)
>>> print(cubes[0].attributes)
{'Conventions': 'CF-1.5'}
>>> print(cubes[1].attributes)
{}
>>> print(cubes[2].attributes)
{}
>>> print(cubes.merge_cube())
Traceback (most recent call last):
...
raise iris.exceptions.MergeError(msgs)
iris.exceptions.MergeError: failed to merge into a single cube.
cube.attributes keys differ: 'Conventions'
>>> equalise_attributes(cubes)
>>> print(cubes[0].attributes)
{}
>>> print(cubes.merge_cube())
air_temperature / (kelvin) (z: 3; y: 4; x: 5)
Dimension coordinates:
z x - -
y - x -
x - - x
Incomplete Data
Merging input cubes with inconsistent dimension lengths can cause misleading results. This is a common problem when merging cubes generated by different ensemble members in a model run.
The misleading results cause the merged cube to gain an anonymous leading dimension. All the merged coordinates appear as auxiliary coordinates on the anonymous leading dimension. This is shown in the example below:
>>> print(cube)
surface_temperature / (K) (-- : 5494; latitude: 325; longitude: 432)
Dimension coordinates:
latitude - x -
longitude - - x
Auxiliary coordinates:
forecast_month x - -
forecast_period x - -
forecast_reference_time x - -
realization x - -
time x - -
Merging Duplicate Cubes
The Iris merge process does not merge duplicate cubes (two or more identical cubes in
the input cubes) by default.
This behaviour can be changed by setting the unique keyword argument
to merge() to False.
Merging duplicate cubes can cause misleading results. Let’s demonstrate these
behaviours and misleading results with the following example.
In this example we have three input cubes.
The first has a scalar z coordinate with value 1, the second has a
scalar z coordinate with value 2 and the third has a scalar z
coordinate with value 1.
The first and third cubes are thus identical.
We will demonstrate the effect of merging the input cubes with unique=False
(duplicate cubes allowed) and unique=True (duplicate cubes not allowed, which
is the default behaviour):
>>> print(cubes)
0: air_temperature / (kelvin) (y: 4; x: 5)
1: air_temperature / (kelvin) (y: 4; x: 5)
2: air_temperature / (kelvin) (y: 4; x: 5)
>>> print(cubes.merge(unique=False))
0: air_temperature / (kelvin) (z: 2; y: 4; x: 5)
1: air_temperature / (kelvin) (z: 2; y: 4; x: 5)
>>> print(cubes.merge()) # unique=True is the default.
Traceback (most recent call last):
...
iris.exceptions.DuplicateDataError: failed to merge into a single cube.
Duplicate 'air_temperature' cube, with scalar coordinates z=Cell(point=1, bound=None)
Notice how merging the input cubes with duplicate cubes allowed produces a result
with four z coordinate values.
Closer inspection of these two resultant cubes demonstrates that the
scalar z coordinate with value 2 is found in both cubes.
Trying to merge the input cubes with duplicate cubes not allowed raises an error highlighting the presence of the duplicate cube.
Single Value Coordinates
Coordinates containing only a single value can cause confusion when combining input cubes. Remember:
The
mergeprocess combines multiple input cubes into a single resultant cube with new dimensions created from the scalar coordinate values of the input cubes.The
concatenateprocess combines multiple input cubes into a single resultant cube with the same number of dimensions as the input cubes, but with the length of one or more dimensions extended by joining together sequential dimension coordinates.
In Iris terminology a scalar coordinate is a coordinate of length 1 which does not describe a data dimension.
Let’s look at two example cubes to demonstrate this.
If your cubes are similar to those below (the single value z coordinate
is not on a dimension) then use merge() to
combine your cubes:
>>> print(cubes[0])
air_temperature / (kelvin) (y: 4; x: 5)
Dimension coordinates:
y x -
x - x
Scalar coordinates:
z 1 meters
>>> print(cubes[1])
air_temperature / (kelvin) (y: 4; x: 5)
Dimension coordinates:
y x -
x - x
Scalar coordinates:
z 2 meters
If your cubes are similar to those below (the single value z coordinate is
associated with a dimension) then use concatenate() to
combine your cubes:
>>> print(cubes)
0: air_temperature / (kelvin) (z: 1; y: 4; x: 5)
1: air_temperature / (kelvin) (z: 1; y: 4; x: 5)
Concatenate¶
Time Units
Differences in the units of the time coordinates of the input cubes probably cause
the greatest amount of concatenate-related difficulties.
In recognition of this, Iris has a helper function,
unify_time_units(), to apply a common time unit to all the input cubes.
To demonstrate using unify_time_units(),
let’s adapt our list of input cubes from the concatenate_cube example from earlier.
We’ll give the input cubes unequal time coordinate units and call
unify_time_units() on the input cubes before concatenating
the input cubes using concatenate_cube():
>>> from iris.util import unify_time_units
>>> print(cubes)
0: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
1: air_temperature / (kelvin) (t: 28; y: 3; x: 4)
2: air_temperature / (kelvin) (t: 31; y: 3; x: 4)
>>> print(cubes[0].coord('t').units)
days since 1990-02-15
>>> print(cubes[1].coord('t').units)
days since 1970-01-01
>>> print(cubes.concatenate_cube())
Traceback (most recent call last):
...
ConcatenateError: failed to concatenate into a single cube.
Dimension coordinates metadata differ: t != t
>>> unify_time_units(cubes)
>>> print(cubes[1].coord('t').units)
days since 1990-02-15
>>> print(cubes.concatenate_cube())
air_temperature / (kelvin) (t: 90; y: 3; x: 4)
Dimension coordinates:
t x - -
y - x -
x - - x
Attributes Mismatch
The concatenate process is affected by attributes mismatch on input cubes
in the same way that the merge process is.
The Attributes Mismatch section earlier in this
chapter gives further information on attributes mismatch.