Seasonal Ensemble Model Plots

This example demonstrates the loading of a lagged ensemble dataset from the GloSea4 model, which is then used to produce two types of plot:

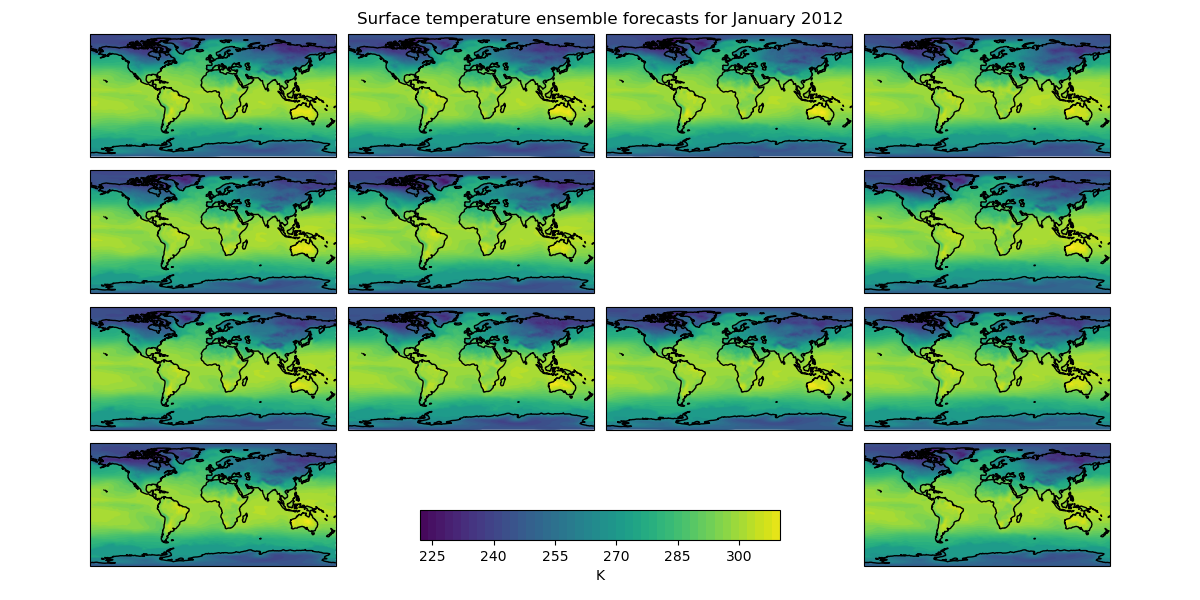
• The first shows the “postage stamp” style image with an array of 14 images, one for each ensemble member with a shared colorbar. (The missing image in this example represents ensemble member number 6 which was a failed run)

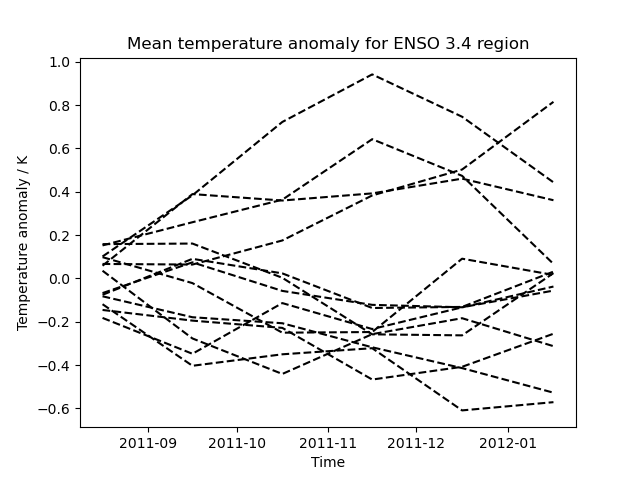
• The second plot shows the data limited to a region of interest, in this case a region defined for forecasting ENSO (El Nino-Southern Oscillation), which, for the purposes of this example, has had the ensemble mean subtracted from each ensemble member to give an anomaly surface temperature. In practice a better approach would be to take the climatological mean, calibrated to the model, from each ensemble member.

• 
• 

import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np

import iris
import iris.plot as iplt


def realization_metadata(cube, field, fname):
    """Modify the cube's metadata to add a "realization" coordinate.

    A function which modifies the cube's metadata to add a "realization"
    (ensemble member) coordinate from the filename if one doesn't already exist
    in the cube.

    """
    # Add an ensemble member coordinate if one doesn't already exist.
    if not cube.coords("realization"):
        # The ensemble member is encoded in the filename as *_???.pp where ???
        # is the ensemble member.
        realization_number = fname[-6:-3]
        realization_coord = iris.coords.AuxCoord(
            np.int32(realization_number), "realization", units="1"
        )
        cube.add_aux_coord(realization_coord)


def main():
    # Create a constraint to extract surface temperature cubes which have a
    # "realization" coordinate.
    constraint = iris.Constraint("surface_temperature", realization=lambda value: True)
    # Use this to load our ensemble.  The callback ensures all our members
    # have the "realization" coordinate and therefore they will all be loaded.
    surface_temp = iris.load_cube(
        iris.sample_data_path("GloSea4", "ensemble_???.pp"),
        constraint,
        callback=realization_metadata,
    )

    # -------------------------------------------------------------------------
    # Plot #1: Ensemble postage stamps
    # -------------------------------------------------------------------------

    # For the purposes of this example, take the last time element of the cube.
    # First get hold of the last time by slicing the coordinate.
    last_time_coord = surface_temp.coord("time")[-1]
    last_timestep = surface_temp.subset(last_time_coord)

    # Find the maximum and minimum across the dataset.
    data_min = np.min(last_timestep.data)
    data_max = np.max(last_timestep.data)

    # Create a wider than normal figure to support our many plots.
    plt.figure(figsize=(12, 6), dpi=100)

    # Also manually adjust the spacings which are used when creating subplots.
    plt.gcf().subplots_adjust(
        hspace=0.05,
        wspace=0.05,
        top=0.95,
        bottom=0.05,
        left=0.075,
        right=0.925,
    )

    # Iterate over all possible latitude longitude slices.
    for cube in last_timestep.slices(["latitude", "longitude"]):
        # Get the ensemble member number from the ensemble coordinate.
        ens_member = cube.coord("realization").points[0]

        # Plot the data in a 4x4 grid, with each plot's position in the grid
        # being determined by ensemble member number.  The special case for the
        # 13th ensemble member is to have the plot at the bottom right.
        if ens_member == 13:
            plt.subplot(4, 4, 16)
        else:
            plt.subplot(4, 4, ens_member + 1)

        # Plot with 50 evenly spaced contour levels (49 intervals).
        cf = iplt.contourf(cube, 49, vmin=data_min, vmax=data_max)

        # Add coastlines.
        plt.gca().coastlines()

    # Make an axes to put the shared colorbar in.
    colorbar_axes = plt.gcf().add_axes([0.35, 0.1, 0.3, 0.05])
    colorbar = plt.colorbar(cf, colorbar_axes, orientation="horizontal")
    colorbar.set_label(last_timestep.units)

    # Limit the colorbar to 8 tick marks.
    colorbar.locator = matplotlib.ticker.MaxNLocator(8)
    colorbar.update_ticks()

    # Get the time for the entire plot.
    time = last_time_coord.units.num2date(last_time_coord.bounds[0, 0])

    # Set a global title for the postage stamps with the date formatted by
    # "monthname year".
    time_string = time.strftime("%B %Y")
    plt.suptitle(f"Surface temperature ensemble forecasts for {time_string}")

    iplt.show()

    # -------------------------------------------------------------------------
    # Plot #2: ENSO plumes
    # -------------------------------------------------------------------------

    # Nino 3.4 lies between: 170W and 120W, 5N and 5S, so use the intersection
    # method to restrict to this region.
    nino_cube = surface_temp.intersection(latitude=[-5, 5], longitude=[-170, -120])

    # Calculate the horizontal mean for the nino region.
    mean = nino_cube.collapsed(["latitude", "longitude"], iris.analysis.MEAN)

    # Calculate the ensemble mean of the horizontal mean.
    ensemble_mean = mean.collapsed("realization", iris.analysis.MEAN)

    # Take the ensemble mean from each ensemble member.
    mean -= ensemble_mean

    plt.figure()

    for ensemble_member in mean.slices(["time"]):
        # Draw each ensemble member as a dashed line in black.
        iplt.plot(ensemble_member, "--k")

    plt.title("Mean temperature anomaly for ENSO 3.4 region")
    plt.xlabel("Time")
    plt.ylabel("Temperature anomaly / K")

    iplt.show()


if __name__ == "__main__":
    main()