Note
Go to the end to download the full example code
Colouring Anomaly Data With Logarithmic Scaling#
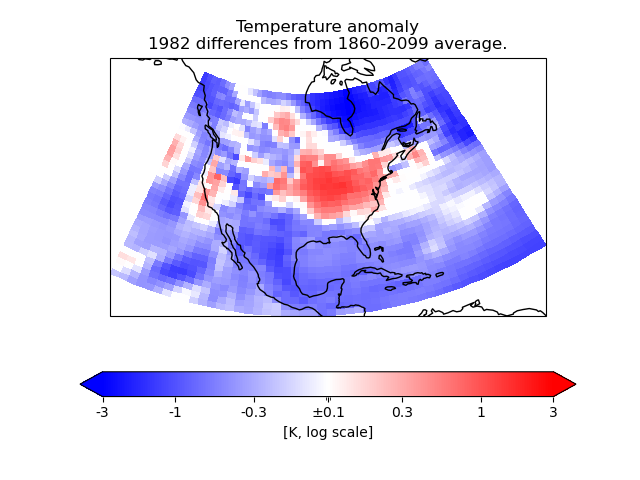
In this example, we need to plot anomaly data where the values have a “logarithmic” significance – i.e. we want to give approximately equal ranges of colour between data values of, say, 1 and 10 as between 10 and 100.
As the data range also contains zero, that obviously does not suit a simple logarithmic interpretation. However, values of less than a certain absolute magnitude may be considered “not significant”, so we put these into a separate “zero band” which is plotted in white.
To do this, we create a custom value mapping function (normalization) using
the matplotlib Norm class matplotlib.colors.SymLogNorm.
We use this to make a cell-filled pseudocolor plot with a colorbar.
Note
By “pseudocolour”, we mean that each data point is drawn as a “cell”
region on the plot, coloured according to its data value.
This is provided in Iris by the functions iris.plot.pcolor() and
iris.plot.pcolormesh(), which call the underlying matplotlib
functions of the same names (i.e., matplotlib.pyplot.pcolor
and matplotlib.pyplot.pcolormesh).
See also: https://en.wikipedia.org/wiki/False_color#Pseudocolor.
import cartopy.crs as ccrs
import matplotlib.colors as mcols
import matplotlib.pyplot as plt
import iris
import iris.coord_categorisation
import iris.plot as iplt
def main():
# Load a sample air temperatures sequence.
file_path = iris.sample_data_path("E1_north_america.nc")
temperatures = iris.load_cube(file_path)
# Create a year-number coordinate from the time information.
iris.coord_categorisation.add_year(temperatures, "time")
# Create a sample anomaly field for one chosen year, by extracting that
# year and subtracting the time mean.
sample_year = 1982
year_temperature = temperatures.extract(iris.Constraint(year=sample_year))
time_mean = temperatures.collapsed("time", iris.analysis.MEAN)
anomaly = year_temperature - time_mean
# Construct a plot title string explaining which years are involved.
years = temperatures.coord("year").points
plot_title = "Temperature anomaly"
plot_title += "\n{} differences from {}-{} average.".format(
sample_year, years[0], years[-1]
)
# Define scaling levels for the logarithmic colouring.
minimum_log_level = 0.1
maximum_scale_level = 3.0
# Use a standard colour map which varies blue-white-red.
# For suitable options, see the 'Diverging colormaps' section in:
# https://matplotlib.org/stable/gallery/color/colormap_reference.html
anom_cmap = "bwr"
# Create a 'logarithmic' data normalization.
anom_norm = mcols.SymLogNorm(
linthresh=minimum_log_level,
linscale=0.01,
vmin=-maximum_scale_level,
vmax=maximum_scale_level,
)
# Setting "linthresh=minimum_log_level" makes its non-logarithmic
# data range equal to our 'zero band'.
# Setting "linscale=0.01" maps the whole zero band to the middle colour value
# (i.e., 0.5), which is the neutral point of a "diverging" style colormap.
# Create an Axes, specifying the map projection.
plt.axes(projection=ccrs.LambertConformal())
# Make a pseudocolour plot using this colour scheme.
mesh = iplt.pcolormesh(anomaly, cmap=anom_cmap, norm=anom_norm)
# Add a colourbar, with extensions to show handling of out-of-range values.
bar = plt.colorbar(mesh, orientation="horizontal", extend="both")
# Set some suitable fixed "logarithmic" colourbar tick positions.
tick_levels = [-3, -1, -0.3, 0.0, 0.3, 1, 3]
bar.set_ticks(tick_levels)
# Modify the tick labels so that the centre one shows "+/-<minumum-level>".
tick_levels[3] = r"$\pm${:g}".format(minimum_log_level)
bar.set_ticklabels(tick_levels)
# Label the colourbar to show the units.
bar.set_label("[{}, log scale]".format(anomaly.units))
# Add coastlines and a title.
plt.gca().coastlines()
plt.title(plot_title)
# Display the result.
iplt.show()
if __name__ == "__main__":
main()
Total running time of the script: (0 minutes 0.485 seconds)
-3.9.0-green?style=flat)